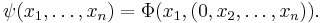Domain-straightening theorem
In differential calculus, the domain-straightening theorem states that, given a vector field  on a manifold, there exist local coordinates
on a manifold, there exist local coordinates  such that
such that 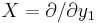 in a neighborhood of a point where
in a neighborhood of a point where  is nonzero. The theorem is also known as straightening out of a vector field.
is nonzero. The theorem is also known as straightening out of a vector field.
The Frobenius theorem in differential geometry can be considered as a higher dimensional generalization of this theorem.
Proof
It is clear that we only have to find such coordinates at 0 in 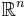 . First we write
. First we write 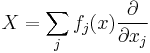 where
where  is some coordinate system at
is some coordinate system at  . Let
. Let 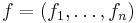 . By linear change of coordinates, we can assume
. By linear change of coordinates, we can assume 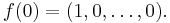 Let
Let 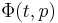 be the solution of the initial value problem
be the solution of the initial value problem 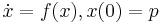 and let
and let
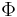 (and thus
(and thus  ) is smooth by smooth dependence on initial conditions in ordinary differential equations. It follows that
) is smooth by smooth dependence on initial conditions in ordinary differential equations. It follows that
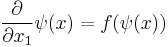 ,
,
and, since 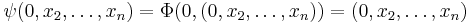 , the differential
, the differential 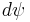 is the identity at
is the identity at  . Thus,
. Thus, 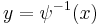 is a coordinate system at
is a coordinate system at  . Finally, since
. Finally, since 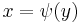 , we have:
, we have: 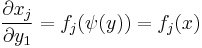 and so
and so 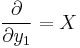 as required.
as required.